Working with voxel fomat

Often imaging data is provided in voxel format. However, as ValoMC uses tetrahedrons as the basis elements, the data are not directly compatible. This example demonstrates how to move between the two formats.

Contents

Creating a rectangular 3d mesh

To create a mesh that can be easily mapped to a voxel grid the function createGridMesh can be used

clear all;

x_arr = -2:1:2;
y_arr = -2:1:2;
z_arr = -2:1:2;

vmcmesh = createGridMesh(x_arr, y_arr, z_arr); % function provided by ValoMC

nvoxels_total = length(x_arr)*length(y_arr)*length(z_arr);
voxels_in_a_yx_slice = length(y_arr)*length(x_arr);

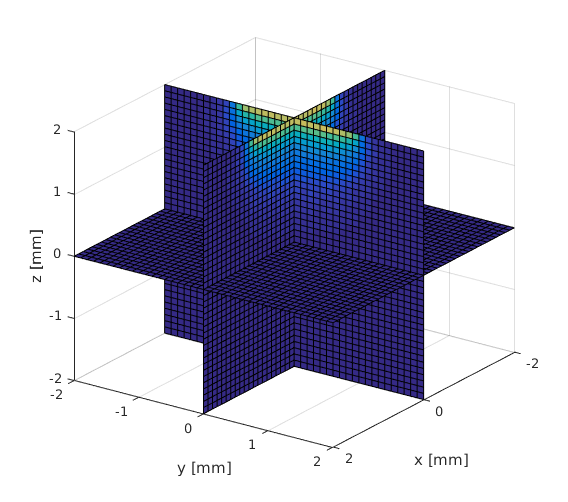
Visualization of the mesh

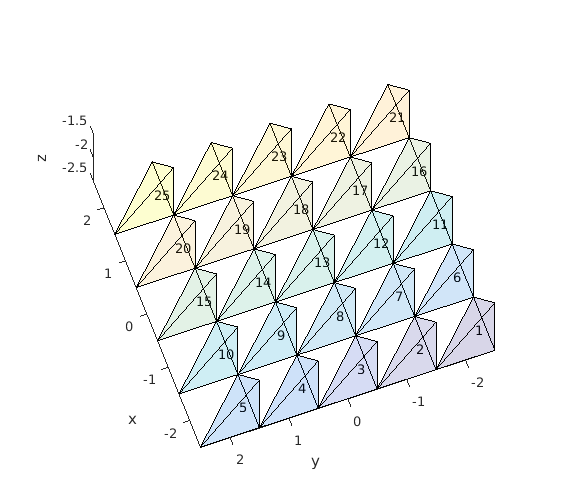
The structure of the mesh is similar as in the 2d version (see pixeltest.m). Each voxel consists of 6 tetrahedrons. Vectors x_arr, y_arr and z_arr contain the center of each voxel. The elements 1 to nvoxels_total contain the first tetrahedron in a voxel, nvoxels_total to 2*nvoxels_total the second and so on. The elements are ordered in the same fashion as the coordinates in meshgrid i.e. Y ascends first, then X and finally Z. Illustration of the element indices is given in the figure below.

tetramesh(vmcmesh.H(1:voxels_in_a_yx_slice,:),vmcmesh.r, 'FaceAlpha', ...
          0.1);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');

% draw the element numbers
for i=1:voxels_in_a_yx_slice
   element_center = (vmcmesh.r(vmcmesh.H(i,1),:) + vmcmesh.r(vmcmesh.H(i,2),:) ...
                     + vmcmesh.r(vmcmesh.H(i,3),:) + vmcmesh.r(vmcmesh.H(i,4),:)) * 0.25;
   text(element_center(1), element_center(2), element_center(3), num2str(i));
end

view(-110,50);
snapnow;
hold off;

% Create a finer mesh

x_arr = -2:0.1:2;
y_arr = -2:0.1:2;
z_arr = -2:0.1:2;

vmcmesh = createGridMesh(x_arr, y_arr, z_arr); % function provided by ValoMC
vmcmedium = createMedium(vmcmesh);

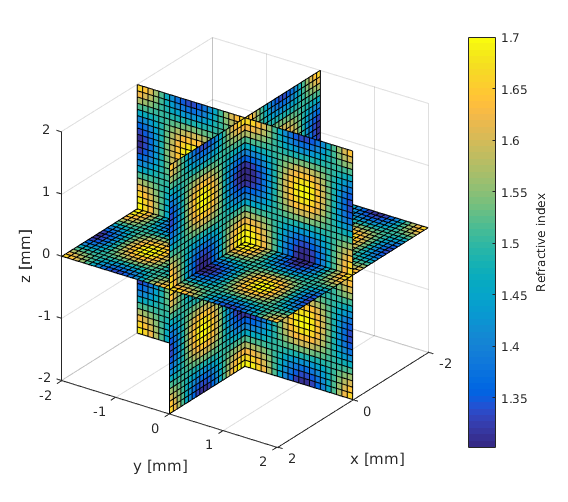
Create an anisotropic parameter distribution

[X,Y,Z] = meshgrid(x_arr,y_arr,z_arr); % Matlab function
F = 1.3+cos(X*3).*cos(Y*3).*cos(Z*3)*0.2+0.2;
slice(X, Y, Z, F, 0, 0, 0);
xlabel('x [mm]');
ylabel('y [mm]');
zlabel('z [mm]');
c=colorbar;
c.Label.String = 'Refractive index';
view(125,25);
snapnow;

Accessing elements using one dimensional indexing

Note that since there are six times as many tetrahedrons as there are grid cells, vmcmedium.absorption_coefficient is six times bigger than F A complete assignment can be achieved by repeating the array F six times

vmcmedium.scattering_coefficient = 1.0;
vmcmedium.absorption_coefficient = repmat(F(:),6,1); % repeat six times

vmcmedium.scattering_anisotropy = 0.9;
vmcmedium.refractive_index = 1;

vmcboundary = createBoundary(vmcmesh, vmcmedium);   % create a boundary for the mesh

% Create a light source
lightsource = findBoundaries(vmcmesh, 'direction', [0 0 0], [0 0 10], 1);
vmcboundary.lightsource(lightsource) = {'cosinic'};


solution = ValoMC(vmcmesh, vmcmedium, vmcboundary);

                 ValoMC-3D
--------------------------------------------
  Version:  v1.0b-118-g853f111
  Revision: 131
  OpenMP enabled                     
  Using 16 threads
--------------------------------------------
Initializing MC3D...
Computing... 
...done

Done

Visualize the solution

TR = triangulation(double(vmcmesh.H),vmcmesh.r); % create a matlab
                                           % triangulation object
                                           % from the mesh

locations = [X(:) Y(:) Z(:)];              % form a 2D matrix from all
                                           % the grid points

indices = pointLocation(TR,locations);     % query the indices of the
                                           % tetrahedrons at grid
                                           % points

indices(isnan(indices)) = 1;               % set the grid points that
                                           % do not belong to the mesh
                                           % to point at the first
                                           % element

% get the values on a grid
grid_fluence = reshape(solution.element_fluence(indices),size(X));


slice(X, Y, Z, grid_fluence, 0, 0, 0);
xlabel('x [mm]');
ylabel('y [mm]');
zlabel('z [mm]');

view(125,25);
snapnow;

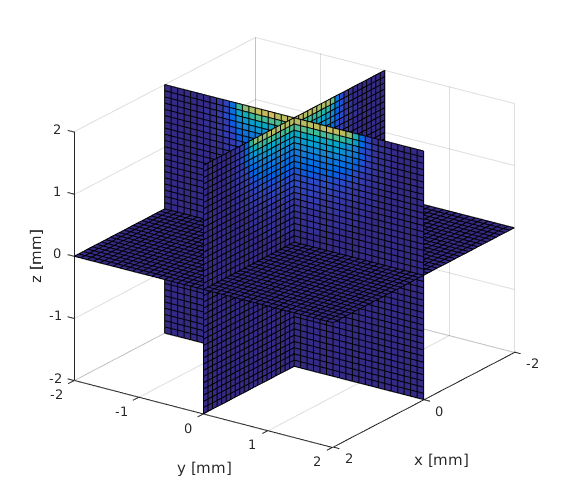
Accessing elements using three dimensional indexing

Optionally, the medium can be defined using three-dimensional indexing. If three dimensional indexing is used, ValoMC will assume that createGridMesh has been used to create the mesh. In addition to the solution.element_fluence, ValoMC will return solution.grid_fluence, which represents the fluence in each voxel. It is calculated as a sum of the tetrahedrons in a grid cell.

clear vmcmedium;
clear vmcboundary;

vmcmedium.scattering_coefficient = 1.0;
vmcmedium.absorption_coefficient = F;  %refractive index is now a three dimensional array
vmcmedium.scattering_anisotropy = 0.9;
vmcmedium.refractive_index = 1;

vmcboundary = createBoundary(vmcmesh, vmcmedium);

lightsource = findBoundaries(vmcmesh, 'direction', [0 0 0], [0 0 10], 1);
vmcboundary.lightsource(lightsource) = {'cosinic'};


solution = ValoMC(vmcmesh, vmcmedium, vmcboundary);

                 ValoMC-3D
--------------------------------------------
  Version:  v1.0b-118-g853f111
  Revision: 131
  OpenMP enabled                     
  Using 16 threads
--------------------------------------------
Initializing MC3D...
Computing... 
...done

Done

Visualize the solution as a voxel map

Since 3D array was used to define the scattering coefficient, solution returned contains the field grid_fluence

slice(X, Y, Z, solution.grid_fluence, 0, 0, 0);
xlabel('x [mm]');
ylabel('y [mm]');
zlabel('z [mm]');
view(125,25);
hold

snapnow;

Current plot held

Published with MATLAB® R2016b